Android Bubble Sort Puzzle Solver
During 2020 summer vacation, I was quite bored.
At some point I noticed a game being played in a smartphone near me.
It was the Ball Sort Puzzle.
I asked to borrow the phone and tried to solve level 159.
Pretty tough if you ask me!
But it shouldn't be, right?
You just try some random moves. You reach a dead end. Then you start again.
You keep trying moves, until you either lock yourself up, or you either solve it.
So you are searching for a chain of moves that take you from the start to the solution ...
This sounds familiar!
You know who's extremely good at this?
Artificial Intelligence!
I like to call myself a Software Engineer so I had to prove (to myself) that this game can be solved with AI. AI created by me. During summer vacation.
Challenge accepted!
Lo and behold my code!
The details
I use a simple plain string to represent the state of the game.
The state string consists of _ to denote an Empty Slot, a character x
to denote a Ball, and (a space) to delimit one tube from another.
There is a mapping in colors.py from actual color names to a hex digit.
Using this trick I can represent a ball using a single character.
Therefore, the following state:
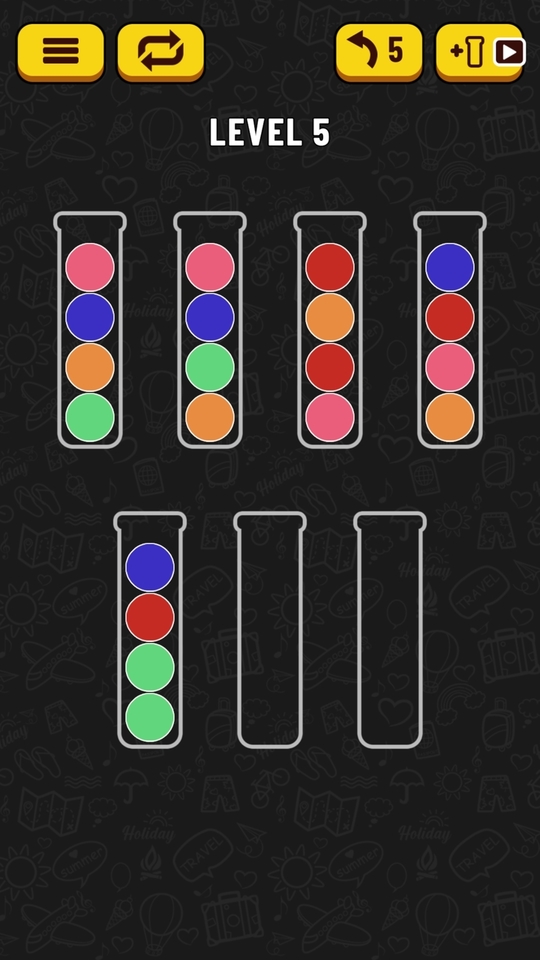
Will translate to the following state string:
8076 8067 a7a8 0a87 0a66 ____ ____
From each state string, a helper method can produce all possible next state strings. This is essentially my transition function. The helper function will also return the move(s) that lead to each next state.
Having an initial state, and a transition function, I can run BFS to search for states that are solutions.
I can keep generating states, and adding them to the frontier, like so:
frontier.add(intitial_state);
while frontier.has_states() {
state = frontier.get_state();
if is_solution(state) {
return;
}
frontier.add(get_next_states(state));
}
When a state is a solution state, the search is over and I return the list of moves associated with this state.
Some states will come up more than once. To save time, I try to prevent states from being re-examined. To do so, I store each visited state, in a Trie data structure. The trie offers fast insertion and lookup.
If a state is "locked", meaning that it cannot produce next states, then OK. I simply discard this state and I do not increase the size of the frontier.
The final piece is the algorithm itself.
I started with a simple Breadth First Search to find the solution with the minimum number of moves.
However, the search space is large enough, so I needed a way to "help" the algorithm a bit.
I used a custom data structure called QuantizedDoubleEndedPriorityQueue.
In simple words, it is a set of double-ended queues. Each queue is associated with a rank. The rank is the number of "solved" tubes.
So as an example, the following state string has rank=3:
8888 _067 _a7a _0a7 0a66 ____ ____
Should I count empty tubes as solved? Good question ...
When the algorithm picks the next state to examine,
the QuantizedDoubleEndedPriorityQueue will always return the state string
with the maximum rank.
Using this technique, the search is more "pointed" towards states that are closer to solution, rather than searching through the entire search space.
Performance
So far, it seems like it can solve levels in under 1sec.
Which is great, because my first iteration on this problem needed more than 60seconds for some levels.
Things to improve in the future
1) Write tests with pytest and achieve 100% coverage
2) The following state strings are effectively the same, right?
8888 _067 _a7a _0a7 0a66 ____ ____
____ _067 _a7a _0a7 0a66 ____ 8888
So, I should treat them as the same, and "prune" the search space. And to do so, I should drop the "move from X to Y" notation, since the ordering of the tubes will make no sense if I shuffle them.